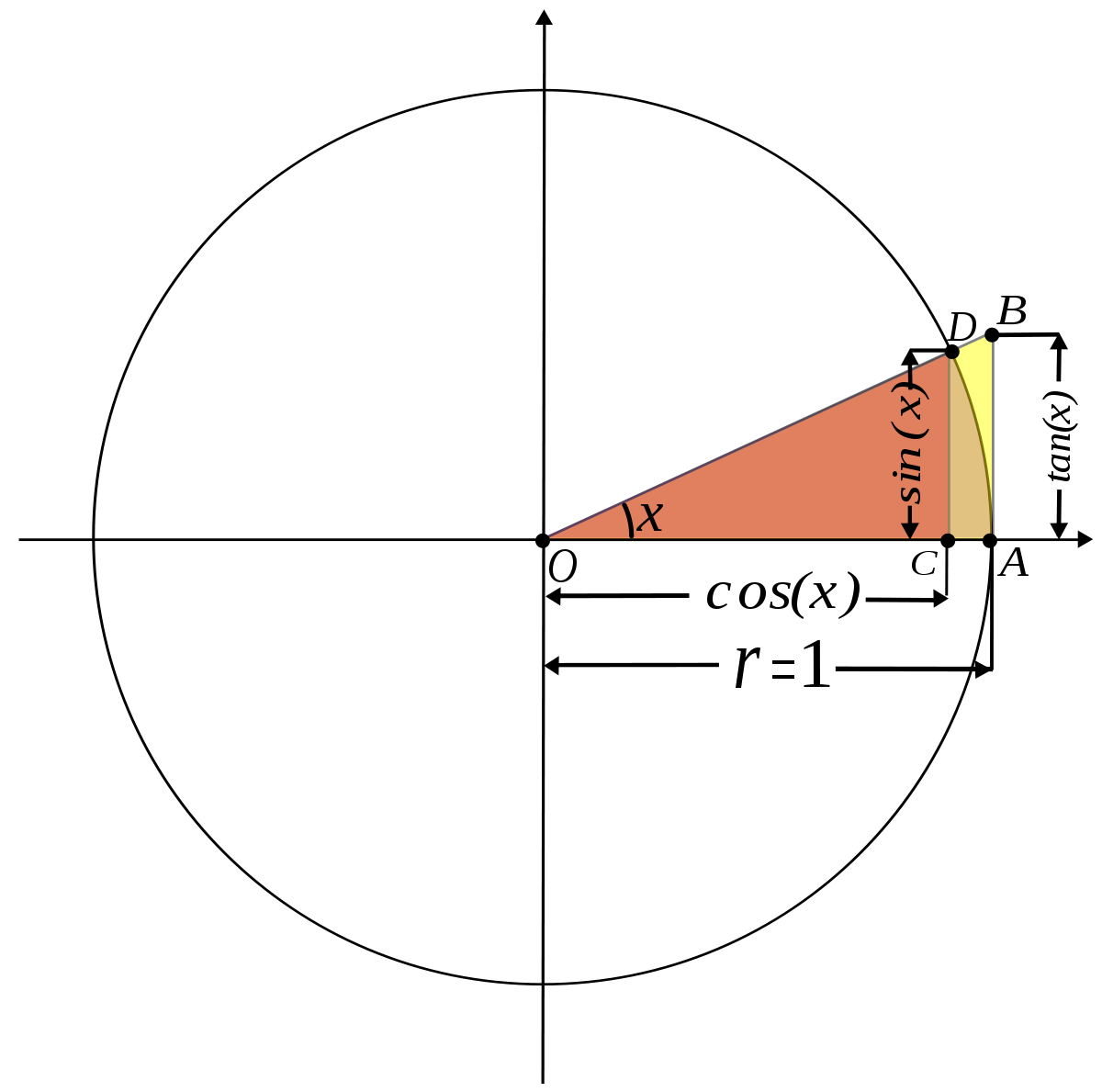
قانون حساب الظل
ويمكن إيجاد ظل الزاوية باتباع الخطوات الآتية:
ظل الزاوية = جيب الزاوية / جيب تمام الزاوية
** جيب الزاوية = الضلع المقابل / الوتر
** جيب تمام الزاوية = الضلع المجاور / الوتر
ظل الزاوية = (الضلع المقابل / الوتر) / (الضلع المجاور / الوتر)
ظل الزاوية = الضلع المقابل / الضلع المجاور
أمثلة على إيجاد ظل الزوايا
فيما يلي مجموعة من الأمثلة التي توضح كيفية إيجاد الظل للزوايا المختلفة:
مثال 1 : ما هو ظل زاوية في المثلث القائم التي يكون الضلع المقابل لها يساوي 12 والضلع المجاور يساوي 16 ؟
الحل: يمكن حل هذا المثال باتباع الخطوات الآتية:
** لحل أي سؤال فإنه يتم تحديد المعطيات كخطوة أولية وهذا يسهل حل السؤال ويختصر الكثير من الوقت والجهد حيث إنه تم إعطاء في السؤال الضلع المقابل ويساوي 12 والضلع المجاور ويساوي 16.
** المراد هو إيجاد ظل الزاوية وكما ذكرنا في الأعلى فإن ظل أي زواية = الضلع المقابل / الضلع المجاور ويساوي 12 / 16 وبتبسيط هذا المقدار إلى أبسط صورة ممكنة فإن ظل الزاوية = 3 / 4.
مثال 2: ما هو ظل زاوية في المثلث القائم التي يكون الضلع المقابل لها يساوي 7 والضلع المجاور يساوي 5 ؟
الحل: يمكن حل هذا المثال باتباع الخطوات الآتية:
** لحل أي سؤال فإنه يتم تحديد المعطيات كخطوة أولية وهذا يسهل حل السؤال كما ذكرنا سابقاً حيث إنه تم إعطاء في السؤال الضلع المقابل ويساوي 7 والضلع المجاور ويساوي 5.
** المراد هو إيجاد ظل الزاوية وكما ذكرنا في الأعلى فإن ظل أي زواية = الضلع المقابل / الضلع المجاور ويساوي 7 / 5 وبالتالي فإن ظل الزاوي يساوي 1.4، ولا يوجد وحدة للظل أو الجيب أو جيب التمام لأنها تمثل النسب بين الأضلاع المثلثية المختلفة.
ملاحظة هامة: تعتبر الزوايا 45، 30، 60 درجة من الزوايا المشهورة التي تستخدم بشكل كبير لذا يقوم الكثيرين بحفظ النسب المثلثية (الظل، والجيب وجيب التمام الخاصة بها) وبالتالي فإن قيمة الظل لهذه الزوايا كما يلي:
** ظا 30 = 3√ / 3
** ظا 60 = 3√
** ظا 45 = 1
فمثلاً إذا تم إعطاء في أي سؤال أن قيمة الظل تساوي 1 يمكن بسهولة معرفة أن هذه الزاوية تساوي 45 درجة، كذلك الأمر بالنسبة للزاويتين 30 و 60.